Triangle Tiling
I saw some figures from this paper on Twitter and thought they looked nice, so I decided to implement the algorithm myself. The paper introduces an algorithm for generating arbitrary triangle tilings: a triangle is scaled and rotated about itself multiple times, by constant scaling factor \(s\) and rotation angle \(A\), such that after some number of scaling and rotation operations \(n\), one side of a transformed triangle aligns with one side of the original triangle. By specifying the lower-left angle of the triangle \(C\), the number of transformations before the sides align \(n\), and the number of arms \(m\), the scaling factor \(s\) and other angles of the triangles are computed. The geometry of the tiling problem is shown below, in which angles are denoted in green and distances are denoted in orange:
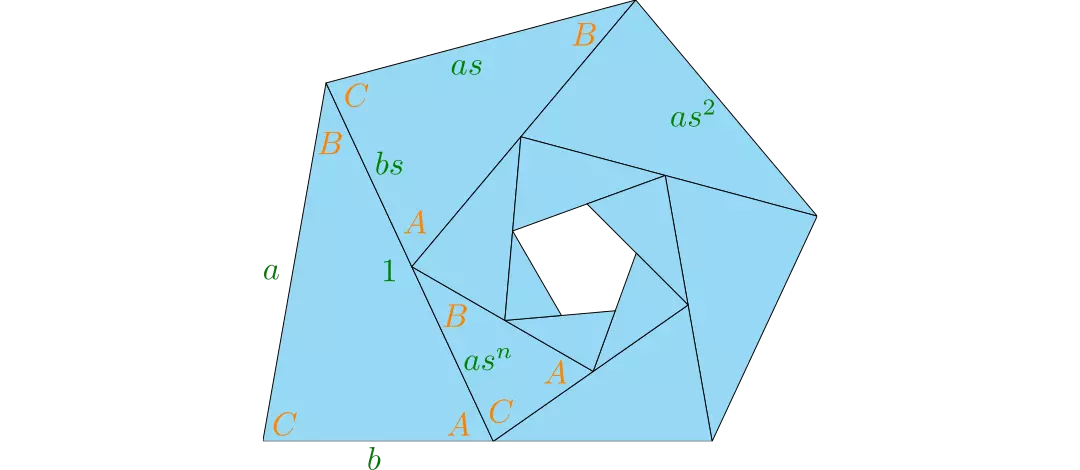 |
|---|
| Diagram of the tiling’s geometry (adapted from Figure 3 of the original paper) |
I implemented the algorithm in Python using NumPy arrays to store and rotate the triangle vertices, SymPy solvers to solve for the scaling factor \(s,\) and Matplotlib to visualize and save the resulting tilings. The figure below shows a comparison of the tilings from the original paper (top) to the tilings generated using my implementation:
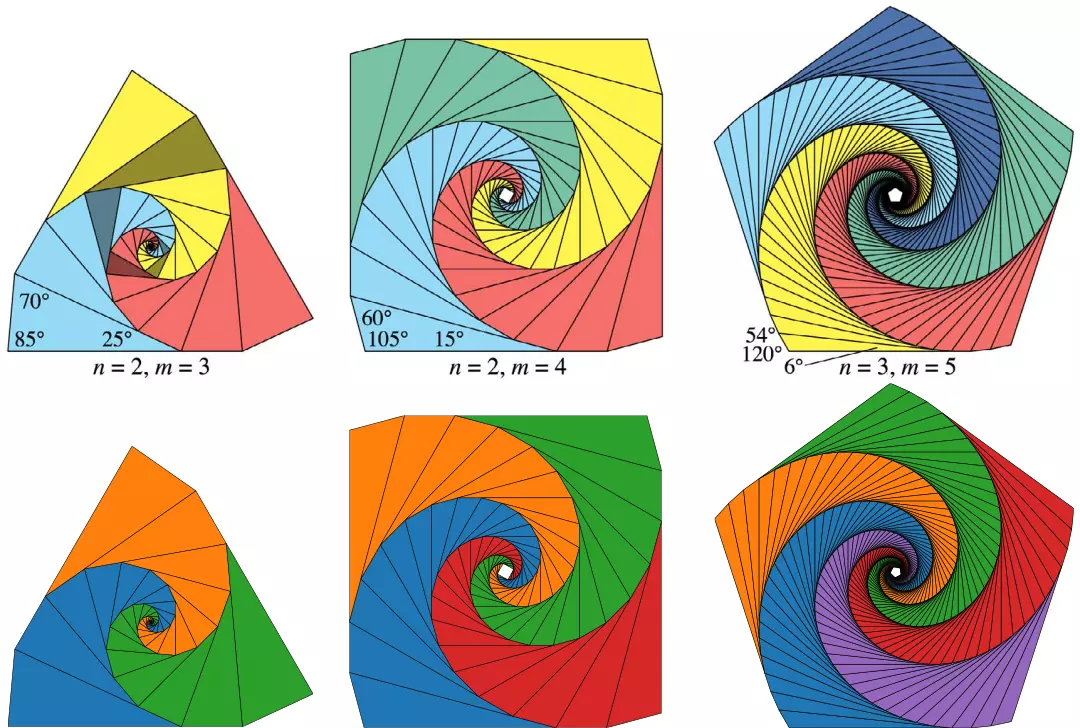 |
|---|
| Comparison of triangle tilings from Figure 14 of the paper (top) and my implementation (bottom) |
Check out the author of the original paper on Twitter or at his website.
